| 중력으로 찌그러진 시공간 | |||||
| 작성자 | 철** | 작성일 | 2019-02-11 | 조회수 | 1260 |
|---|---|---|---|---|---|
|
블랙홀 여행 (3)
목차지난 글에서는 평탄한 4차원 시공간에 대한 이야기를 했다. 그럼 평탄하지 않고 찌그러진 4차원 시공간도 존재할까? 일찍이 아인슈타인은 중력을 다른 힘들과 달리 시공간이 찌그러져 나타나는 현상으로 보았다. 이로부터 빛이 태양의 중력에 의해 휘어질 것이란 예견을 하였고, 이는 에딩턴의 관측으로 보기 좋게 사실로 드러났다. 존 휠러는 이를 설명하기 위해 또 한 번 멋진 표현을 만들어 냈는데, 이는 지금까지도 아인슈타인의 장방정식을 설명하는 최고의 문장으로 여겨지고 있다. 구면좌표계와 지형x축, y축, z축으로 대변되는 직교좌표계는 천문학에서는 그다지 환영받지 못하는 좌표계다. 지구만 봐도 위도와 경도로 위치를 표시하지 어느 누구도 지구를 중심으로 x좌표, y좌표, z좌표를 얘기하지 않는다. 블랙홀 지형도도 마찬가지다. 블랙홀은 별이 강력한 중력에 의해 찌그러져서 만들어지므로 당연히 별처럼 동그란 모습을 가졌을 것이라 여겨진다. 동그랗던 별이 찌그러져 주사위 모양이나 삼각뿔 모양으로 변하지는 않을 것이기 때문이다. 그래서 블랙홀 주변의 지형도를 그리려면 구면좌표계를 쓰는 것이 훨씬 편리하다. 아래 그림에서 보는 바와 같이 구면좌표계에서는 x,y,z 대신에 그럼 3차원 직교좌표계에서 거리를 나타내는 식 직교좌표계를 사용한 식 그럼 좌표계 변환에 의해 생긴 계량함수인지, 아니면 공간이 휘어져 생긴 계량함수인지는 어떻게 알 수 있을까? 이는 공간의 곡률을 계산해 보면 알 수 있다. 애초에 평탄한 공간이라면 좌표계를 어떻게 바꾸어 쓰던가에 상관없이 늘 곡률이 0으로 나온다. 당연히 구면좌표계에서 나타나는 계량함수를 넣어서 곡률을 계산해보면 0이 나온다. 불행히도 곡률의 실제 계산은 매우 복잡하여 이 글에서 다루기에는 적합하지 않다. 그래서 곡률의 계산은 다루지 않도록 하겠다. 어차피 지도를 볼 줄 알면 되지 지도를 그리는 일까지 배울 필요는 없으니까. 슈바르츠실트의 해4차원 민코프스키 공간에서 두 사건 간의 간격을 나타내는 공식을 다시 한 번 들여다보자. 이 식은 직교좌표계를 써서 쓴 식이고, 이를 방금 전에 배운 구면좌표계로 바꿔 쓰면 어떻게 표현될까? 쉽게 예상할 수 있듯이 ‘공간상의 거리’ 부분만 살짝 바꿔주면 된다. 반복되는 이야기이지만, 좌표계만 바뀌었을 뿐 공간의 성격이 바뀐 것은 아니니, 여전히 곡률이 0인 평탄한 민코프스키 시공간이다. 이제 블랙홀 주변의 시공간 지형이 어떤 모습을 하고 있을지를 생각해보자. 블랙홀 주변의 시공간이 등고선과 같이 찌그러져 있음을 표현하기 위해서는 간단히 ‘지형을 나타내는 함수’ 즉 계량(metric)을 넣어주면 될 것이다. 그러기 위해서 가장 간단한 구조를 갖는 블랙홀을 생각해 보자. 가장 간단한 블랙홀이란 회전 운동을 하지 않으면서, 완전한 구형이고, 또 질량의 변화가 없는 정적인 블랙홀일 것이다. 물리학자들은 이렇게 단순한 블랙홀을 ‘슈바르츠실트 블랙홀’이란 복잡한 이름으로 부른다. 슈바르츠실트는 불운했던 한 천재 물리학자의 이름이다. 그는 1915년에 아인슈타인이 장방정식을 발표하자마자 곧바로 그 방정식의 해를 구해 아인슈타인에게 알려줬다고 한다. 당시 슈바르츠실트는 마흔 살이 넘은 나이로 1차 세계대전에 나가 전쟁을 치루면서도 아인슈타인의 장방정식을 풀어냈다고 하니 실로 놀라운 일이 아닐 수 없다. 슈바르츠실트 블랙홀은 시간에 따라 모양의 변화가 없는 정적인 블랙홀이므로 이를 표현하는 계량함수는 시간과는 무관할 것이다. 또 완전한 구형이라서 위도나 경도 방향으로는 공간의 성격이 대칭적일 것이고, 그래서 계량함수가 위도나 경도의 함수도 아닐 것이다. 따라서 계량함수는 오로지 블랙홀과의 거리만의 함수가 될 것이다. 이를 가장 일반적인 수식으로 표현하면, 이 된다. 여기서 A(r)과 B(r)은 각기 시간과 공간을 찌그러뜨리는 정도를 나타내는 계량함수다. 그렇다면 A(r)과 B(r)이 어떤 함수 꼴을 갖는지를 알아내야 하는데, 이를 위해서는 아인슈타인의 장방정식을 풀 필요가 있다. 슈바르츠실트가 한 일이 바로 이 계량함수를 얻어낸 것인데, 그의 풀이에 의하면 A(r)과 B(r)은 서로 역수인 관계가 있고, 그 결과를 쓰면 다음과 같다. 이 계산을 종이와 연필만 가지고 하게 되면, 꽤 많은 단계를 거쳐야 하는데, 다행히도 요즘은 ‘매스매티카(Mathematica)’란 컴퓨터 프로그램이 있어 누구나 쉽게 해낼 수 있다. 그리고 실제 이 과정을 경험해 본 사람이라면, 컴퓨터의 도움도 없이 그것도 100년 전에 이 문제를 풀어낸 슈바르츠실트의 위대함에 놀랄 수밖에 없을 것이다. 불행히도 슈바르츠실트는 이 장방정식의 해를 구하고 이듬해인 1916년에 피부면역질환의 일종인 천포창이란 희귀병에 걸려 세상을 떠났다고 한다. 그를 잃은 것은 단지 그의 개인적인 불운을 넘어 인류사의 큰 손실이 아닐 수 없다. 슈바르츠실트의 해를 가만히 쳐다보면, 어디서 많이 본 식이 하나 들어 있다. 바로 이제부터 본격적으로 이 식을 이용해 블랙홀의 지형도를 살펴보자. 중력 때문에 시간이 늦게 간다.먼저 정량적인 감을 잡기 위해, 슈바르츠실트의 해를 지구에 살고 있는 우리에게 적용해 보자. 일상 속에서 나타나는 우리들의 움직임은 몇 가지 형태로 나눠 볼 수 있다. ![[그림4] (a) 가만히 앉아있는 경우는 공간상의 위치변화가 없다. (b) 지표면에서 걸어다는 경우에는 위도와 경도의 변화만 있을 뿐 지구중심에서 떨어진 거리의 변화는 없다. (c) 엘리베이터를 타고 위아래로 움직이는 경우는 지구중심에서의 거리만 변한다. 세 가지 운동 모두 시간은 흘러가므로 항상 dt는 0이 될 수 없다.](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814115614524_GSXV4MRK1.png/134729_i4.png?type=w530_fst_n&wm=Y)
[그림4] (a) 가만히 앉아있는 경우는 공간상의 위치변화가 없다. (b) 지표면에서 걸어다는 경우에는 위도와 경도의 변화만 있을 뿐 지구중심에서 떨어진 거리의 변화는 없다. (c) 엘리베이터를 타고 위아래로 움직이는 경우는 지구중심에서의 거리만 변한다. 세 가지 운동 모두 시간은 흘러가므로 항상 dt는 0이 될 수 없다. 첫 번째는 카페에 앉아 커피를 마실 때나 잠을 잘 때처럼 아예 움직이지 않을 때다. 이때는 지구 중심으로부터의 거리도 변하지 않고, 위도와 경도 위치도 바뀌지 않으므로 당연히 세 번째로는 엘리베이터를 타고 높은 건물을 오르내리는 경우다. 이때는 위도와 경도에는 변함이 없고, 오로지 지구 중심으로부터의 거리만 변하게 된다. 따라서 이를 수식으로 표현하면 움직이지 않고 가만히 있는 경우에 일반상대성이론은 우리에게 어떤 결과를 가져다줄지 살펴보자. 간단히 그런데 갑자기 튀어나온 ‘고유시간’이란 뭐고 또 ‘좌표시간’이란 뭘까? 좌표시간이란 우리가 처음 설정한 좌표계 별에서 아주 멀리 떨어져 있는 경우는 r값이 매우 크다고 보면 되고, 따라서 위의 두 식을 합쳐보면, 최종적으로 지구의 경우를 예를 들어 내비게이션은 일반상대론을 알고 있다실제로 이 시간 지연효과는 GPS(Global Positioning System) 작동원리 속에 고스란히 녹아들어가 있다. GPS위성은 지표면에서 약 2만km 상공에 떠 있고, 이를 바탕으로 일반상대론에 의한 시간 지연을 계산해보면, GPS위성 속의 시계는 지표면의 시계보다 하루에 45 마이크로초 (0.000045초) 정도 빨리 감을 알 수 있다. 반대로 지표면의 시계가 GPS위성 속의 시계보다 하루에 45마이크로초 늦게 간다고 말해도 된다. 한편 GPS위성은 시간당 14,000km란 엄청난 속도로 움직이고 있어 특수상대성이론에 따라 하루에 약 7마이크로초 정도 시간이 늦게 간다. 그래서 이 효과를 감안하면 GPS의 시계는 지표면 위의 시계보다 38 마이크로초 정도 더 빨리 감을 알 수 있다. 자동차의 내비게이션이 지도위에서 자신의 위치를 알아내는 방법은 순전히 GPS가 보내주는 시각(時刻) 정보에 의존한다. 여러 GPS가 보내주는 서로 다른 시각을 바탕으로 GPS위성들과 자동차와의 거리를 계산해 내는 것인데, 만약 하루에 38마이크로초씩 발생하는 이 시간 지연효과를 보정해주지 않으면, 내비게이션은 무용지물이 되고 만다. 다행히 내비게이션이 일반상대론과 특수상대론에 의한 보정을 잘 처리하고 있어, 우리는 안심하고 내비의 안내에 따라 운전만하면 된다. 찌그러진 공간그럼 공간도 중력에 의해 찌그러들까? 당연하다. 예를 들어 1m짜리 자를 수직으로 들고 있는 사람의 모습을 사진으로 찍었다고 가정해보자. 사진 속 1m 자의 맨 위 부분과 아래 부분의 좌표를 비교해보면, 지구 중심으로부터의 거리 차이는 1m이고, 위도와 경도 차이는 없다. 따라서 사진은 어느 한 순간의 시간좌표에서 찍은 것이므로 dt=0으로 놓고, 이 자의 양쪽 끝 4차원 좌표의 간격을 구해 위 식에서 r이 슈바르츠실트 반경보다 큰 경우를 생각해보면, 분모는 항상 1보다 작다. 따라서 ds > dr 이 된다. 이는 곧 고유길이가 좌표길이보다 크다는 얘기가 된다. 이를 뒤집어 말하면 좌표길이가 고유길이보다 작다는 것이다(그림 참조). 이는 마치 특수상대성이론에서 움직이는 물체의 길이가 줄어드는 것에 비교될 수 있어, 중력에 의한 길이 수축이라 해석될 수도 있다. 다만 특수상대성이론과는 다르게 dr은 우리에게 보이는 양이 아니다. 우리가 관측할 수 있는 길이는 고유길이뿐이다. 우리에게 보이는 1m 자는 고유거리 1m인 것이다. [네이버 지식백과] 중력으로 찌그러진 시공간 - 블랙홀 여행 (3) (물리산책, 박인규)
|
|||||
-
이전글
- 서피스 허브
-
다음글
- 이성 중심적 금욕주의

![[그림1] 평탄하지 않고 등고선과 같이 휘어진 시공간을 표현한 개념도](https://dthumb-phinf.pstatic.net/?src=%22https%3A%2F%2Fdbscthumb-phinf.pstatic.net%2F4749_000_6%2F20170814115614531_M3Q4MIBHS.jpg%2F134729_i1.jpg%3Ftype%3Dw690_fst%26wm%3DN%22&twidth=690&theight=433&opts=17)
![[그림2] 한 점 P는 직교좌표계에선 x,y,z로, 구면좌표계에선 로 표시 된다.](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814122220387_3JTTUBMZS.jpg/134729_i2.jpg?type=h345_fst_n&wm=Y)
![[그림3] 구면좌표계에서의 미소 변위. 가로, 세로, 높이를 라 볼 수 있다.](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814115614526_XDSWOMWYA.png/134729_i3.png?type=h345_fst_n&wm=Y)
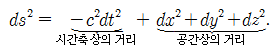
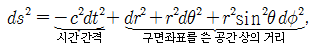
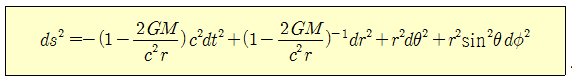
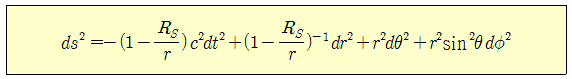
![[그림5] GPS 위성 속의 시계와 지표면 위의 시계는 서로 다르게 간다.](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814122255380_FMPH18MBH.jpg/134729_i5.jpg?type=w530_fst_n&wm=Y)
![[그림6] 1m 자를 들고 서 있는 사람의 사진.](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814115614522_J9SU9V51S.png/134729_i6.png?type=h227_fst_n&wm=Y)
![[그림7] 고유길이와 좌표길이와의 관계](https://dbscthumb-phinf.pstatic.net/4749_000_6/20170814115614535_FCHSXNQWW.png/134729_i7.png?type=w460_fst_n&wm=Y)